Python セットの仕組みと使い方のサンプル(set)

Pythonのセットの仕組みと使い方のサンプルです。(確認環境:Python 3)

サンプル	セット
	セットを作成する
	値を追加する(add)
	値を削除する(remove)
	要素数を取得する(len)
	和集合を求める (union,\|演算子)
	差集合を求める (difference,-演算子)
	積集合を求める (intersection,&演算子)
	排他的論理和集合を求める (symmetric_difference,^演算子)
	セットAの全ての要素は、セットBに含まれているか(issubset,<=)
	セットに特定の要素が含まれているか比較する(in)
	要素の値の最大値、最小値、合計、要素の長さ (max,min,sum,len)
	リストからセットに変換する(set)

セット

変数 = { 値1 , 値2 , 値3 , ... }

1つの変数で複数の値を保持できます。
→各項目を要素(element)といいます。
値の重複は不可です。代入しようとしても追加されません。
順序がありません。
セットは集合とも呼ばれます。
以下はPythonの公式ドキュメントのセットのリンクです。
https://docs.python.jp/3/tutorial/datastructures.html#sets

セットを作成する

# coding: utf-8

s1 = {"赤","黄","青"}

print (s1) # {'青', '黄', '赤'}

s2 = set(["紫","白","黒"])

print (s2) # {'白', '黒', '紫'}

3行目は、セットを作成しています。波かっこ({ })を使用します。
5行目は、変数の値を表示しています。{'青', '黄', '赤'}と表示されています。
7行目は、角括弧([ ])でくくったリストからset関数を用いてセットを作成しています。

値を追加する(add)

# coding: utf-8

s1 = {"赤","黄","青"}

s1.add('オレンジ')

print(s1) #{'青', '黄', 'オレンジ', '赤'}

5行目はaddメソッドでセットに要素を追加しています。

値を削除する(remove)

# coding: utf-8

s1 = {"赤","黄","青"}

s1.remove('黄')

print(s1) #{'赤', '青'}

5行目はremoveメソッドでセットから要素を削除しています。

要素数を取得する(len)

# coding: utf-8

c1 = {"赤","黄","青"}

print(len(c1)) # 3

lenは要素の数を返します。

和集合を求める (union,|演算子)

和集合とは、重複がない集合のことです。

# coding: utf-8

s1 = {"赤","黄","青"}
s2 = {"紫","白","青"}

s3 = s1.union(s2)

print(s3) #{'黄', '赤', '紫', '青', '白'}

print(s1|s2) #{'黄', '赤', '紫', '青', '白'}

6行目はunionメソッドで和集合を返します。青が重複していますが青は1つのみ表示されます。
10行目のように s1|s2とすることもできます。

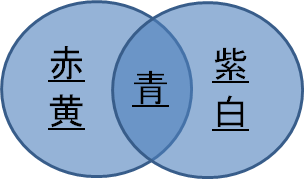
この図は、上記コードの和集合のイメージです。

差集合を求める (difference,-演算子)

差集合とは、要素を引き算した集合のことです。

# coding: utf-8

s1 = {"赤","黄","青"}
s2 = {"紫","白","青"}

s3 = s1.difference(s2)

print(s3) #{'黄', '赤'}

print(s1-s2) #{'黄', '赤'}

6時間行目はdifferenceメソッドで差集合を返します。 s1からs2に青があるので青を除いた赤と黄が表示されます。
10行目のように s1-s2とすることもできます。

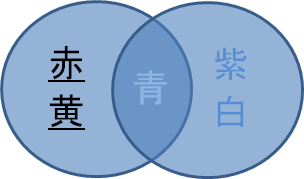
この図は、上記コードの差集合のイメージです。

積集合を求める (intersection,&演算子)

積集合とは、両方のセットにある要素の集合のことです。

# coding: utf-8

s1 = {"赤","黄","青"}
s2 = {"紫","白","青"}

s3 = s1.intersection(s2)

print(s3) #{'青'}

print(s1&s2) #{'青'}

6行目はintersectionメソッドで共通集合(積集合)を返します。両方に含まれる青が表示されます。
10行目のように s1&s2とすることもできます。

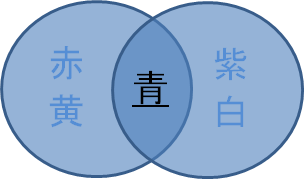
この図は、上記コードの積集合のイメージです。

排他的論理和集合を求める (symmetric_difference,^演算子)

排他的論理和集合とは、どちらか一方のみに含まれる集合のことです。

# coding: utf-8

s1 = {"赤","黄","青"}
s2 = {"紫","白","青"}

s3 = s1.symmetric_difference(s2)

print(s3) #{'紫', '赤', '黄', '白'}

print(s1^s2) #{'紫', '赤', '黄', '白'}

6行目はsymmetric_differenceメソッドで対称的差集合を返します。どちらか一方のみに含まれる紫、赤、黄、白が表示されます。
10行目のように s1^s2とすることもできます。

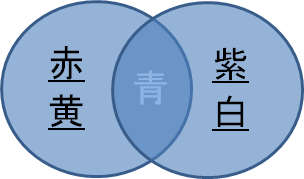
この図は、上記コードの排他的論理和集合のイメージです。

セットAの全ての要素は、セットBに含まれているか(issubset,<=)

# coding: utf-8

s1 = {"赤","黄","オレンジ","青"}
s2 = {"赤","青"}

print(s2.issubset(s1)) # true
print(s2<=s1) # true

issubsetメソッドは、セットA(s2)の全ての要素は、セットB(s1)に含まれているか確認できます。
s2<=s1とすることもできます。

セットに特定の要素が含まれているか比較する(in)

# coding: utf-8

a = {"赤","黄","青"}

b = "赤"

c = {"赤","青"}

if b in a:
	print("含まれる1") #表示される

if c <= a:
	print("含まれる2") #表示される

9行目は、赤という値が3行目のセットに含まれているかin演算子を使用して比較しています。含まれているので文字が表示されます。
12行目は、7行目のセットは、3行目のセットに含まれているか比較演算子の<=を使用して比較しています。含まれているので文字が表示されます。

要素の値の最大値、最小値、合計、要素の長さ (max,min,sum,len)

# coding: utf-8

a = {2,8,3}

print (max(a)) # 8 最大値
print (min(a)) # 2 最小値
print (sum(a)) # 13 合計
print (len(a)) # 3 要素の長さ

lenは要素の長さを返します。

リストからセットに変換する(set)

# coding: utf-8

a = ["赤","黄","青","赤"]

b = set(a)

print (b) # {'黄', '青', '赤'}

3行目は、リストです。
5行目は、setメソッドでリストをセットに変換しています。
重複している値は、削除されます。
7行目の値の順番はランダムです。